Question

NO LINKS!! Which of the following formulas defines an arithmetic sequence?​

Answer 1

`\textsf{c)} \quad s_n=18+7(n-3)`

Step-by-step explanation:

An arithmetic sequence has a constant difference between each term.

General formula of an arithmetic sequence

`\boxed{s_n=a+(n-1)d}`

where:

• sₙ is the nth term.
• a is the first term.
• d is the common difference between terms.
• n is the position of the term.

When expanded, the formulas for answer options a and b will both contain an n² term, so we can immediately discount them since an arithmetic sequence is linear.

Similarly, we can also discount option d since this formula includes an exponential term and is therefore not linear.

Therefore, the only valid answer is option c.

To confirm, rewrite the formula for c in the general form for an arithmetic sequence:

`\begin{aligned}\implies s_n&=18+7(n-3)\\s_n&=18+7n-21\\s_n&=7n-3\\s_n&=7n-7+4\\s_n&=7(n-1)+4\\s_n&=4+(n-1)7\end{aligned}`

Therefore, formula that defines an arithmetic sequence is:

`\boxed{s_n=18+7(n-3)}`

Answer 2

Answer: Choice C

18+7(n-3)

=======================================================

Step-by-step explanation:

We can rewrite the right hand side of choice C like so

18+7(n-3)

18+7(n-1-2)

18+7(n-1)+7(-2)

18+7(n-1)-14

4+7(n-1)

Which is now in the form a+d(n-1)

• a = 4 = first term
• d = 7 = common difference

This confirms choice C to be arithmetic. The other choices cannot be written in the format of a+d(n-1). Choices A and B are quadratic sequences while choice D is exponential.

The first few terms of choice C are: 4, 11, 18, 25, 32, ...

To get new terms, add 7 to the previous one.

-------------

Notice how if n = 5 for instance, then,

`a_n = 4+7(n-1)\\\\a_5 = 4+7(5-1)\\\\a_5 = 32\\\\`

and

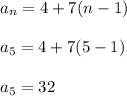
`b_n = 18+7(n-3)\\\\b_5 = 18+7(5-3)\\\\b_5 = 32\\\\`

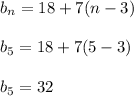
This confirms that
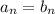`a_n = b_n` when n = 5. I'll let you check other positive integer values for n.