Question

NO LINKS! PLEASE help me with this problem 2f​

Answer 1

`\textsf{c)} \quad u_1=43, \quad d=3`

Explanation:

General formula of an arithmetic sequence

`\boxed{u_n=u_1+(n-1)d}`

where:

• uₙ is the nth term.
• u₁ is the first term.
• d is the common difference between terms.
• n is the position of the term.

Given terms:

• u₂₀ = 100
• u₂₅ = 115

Substitute the given terms into the formula to create two equations:

`\begin{aligned}\implies u_(20)=u_1+(20-1)d&=100\\u_1+19d&=100\end{aligned}`

`\begin{aligned}\implies u_(25)=u_1+(25-1)d&=115\\u_1+24d&=115\end{aligned}`

Subtract the first equation from the second equation to eliminate u₁:

`\begin{array}{rrclcl}& u_1 &+ &24d &= &115\\-& (u_1 &+ &19d& =& 100)\\\cline{2-6}&&&5d &=& \phantom{1}15\end{array}`

Solve for d:

`\implies 5d=15`

`\implies (5d)/(5)=(15)/(5)`

`\implies d=3`

Substitute the found value of d into one of the equations and solve for u₁:

`\implies u_1+19(3)=100`

`\implies u_1+57=100`

`\implies u_1=43`

Therefore:

• u₁ = 43
• d = 3

Answer 2

Answer: Choice C

`u_1 = 43, \ d = 3`

=======================================================

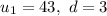
Work Shown:

a =
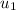`u_1` = first term

d = common difference

Let's start off plugging in n = 20 and then isolating the variable 'a'

`u_n = u_1 + d(n-1)\\\\u_(20) = a + d(20-1)\\\\100 = a + 19d\\\\a = 100-19d\\\\`

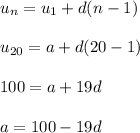
We'll come back to it later.

Now plug in n = 25

`u_n = u_1 + d(n-1)\\\\u_(25) = a + d(25-1)\\\\115 = a + 24d\\\\a+24d = 115\\\\`

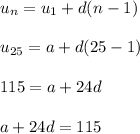
Let's replace each copy of 'a' with 100-19d, because of the equation we solved for earlier.

`a+24d = 115\\\\100-19d+24d = 115\\\\100+5d = 115\\\\5d = 115-100\\\\5d = 15\\\\d = 15 / 5\\\\d = 3\\\\`

Now we can finally determine 'a'

`a = 100-19d\\\\a = 100-19*3\\\\a = 100-57\\\\a = 43\\\\`

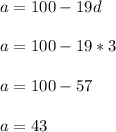
which is the first term.

To quickly list out the terms, I recommend using a spreadsheet. That way you can confirm the answers.

-----------------------

Another way to check the answer is to plug n = 20 into
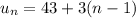`u_n = 43 + 3(n-1)` and you should get
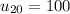`u_(20) = 100`. Also, plugging n = 25 into that formula should yield
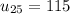`u_(25) = 115`. These two facts fully confirm the answer. I'll let you perform this check.