Answer: Choice A
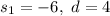
==================================================
Work Shown:
a =
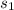 = first term
= first term
d = common difference
Plug n = 5 into the arithmetic sequence formula to get...
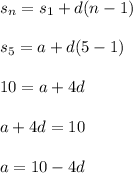
Do similar steps for n = 8
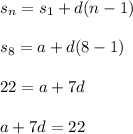
Now plug in a = 10-4d and solve for d.
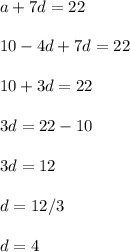
The common difference is d = 4. This narrows the answer choices between A and D.
Use d = 4 to find 'a'.
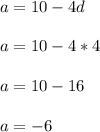
Alternatively you could use the other equations that had 'a' and 'd' in them.
------------------
The first term is a = -6 and the common difference is d = 4
The arithmetic sequence is:
-6, -2, 2, 6, 10, 14, 18, 22, ...
The terms in bold represent the 5th and 8th terms respectively. They are highlighted to help confirm the answers.
It might help to make a table like this

or like this

Each time you need a new term, add on 4.