Answer:
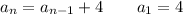
Explanation:
You want the recursive formula that matches the sequence 4, 8, 12, 16, 20.
Recursive formula
Your problem statement tells you the recursive formula is ...

where 'd' is the common difference.
This means you only need to identify the perimeter associated with n=1 (first term), and the difference between perimeters for adjacent values of n.
The table tells you ...

Filling these values into the given formula, you have the recursive formula ...
