Question

The integral of

f(x)=100x^99+20x^4+2/x^2+3/x+9

is

Answer 1

(a)

Explanation:

You want to identify the integral of f(x)=100x^99+20x^4+2/x^2+3/x+9.

Power rule

For all powers of x except x^-1 = 1/x, the power rule applies:

`\int{x^n}\,dx=(x^(n+1))/(n+1)`

Logarithm

The power rule cannot apply when n=-1, as that would make the integral undefined. Instead, the integral is ...

`\int{x^(-1)}\,dx=ln((x))`

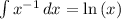
Constants

Any constant multiplier (k) of the expression being integrated will be a constant multiplier of the integral of that expression.

Any indefinite integral may have a constant (c) added.

`\displaystyle k\cdot\int{f'(x)}\,dx=k\cdot f(x)+c`

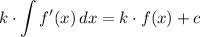
Applying these rules, we get the integral shown in the attachment.