Answer:
2 real different roots
Explanation:
Discriminant determines the number of real solutions of a quadratic equation. The formula of discriminant goes by:
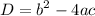
The formula is derived from a quadratic formula which is:

The expression inside the square root is discriminant. The discriminant says that:
- There are 2 real different roots if the discriminant (D) is greater than 0. (D > 0)
- There is 2 real double roots (same roots) if the discriminant (D) is equal to 0. (D = 0)
- There are no real roots (imaginary or complex roots) if the discriminant (D) is less than 0. (D < 0)
From the equation
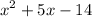 , determine the coefficients of equation:
, determine the coefficients of equation:
Therefore, substitute the coefficients’ values in the discriminant:

Since the discriminant is greater than 0, we can conclude that this equation will have 2 real different roots.