Answer:
20 seconds
360 meters
Step-by-step explanation:
On a distance-time graph:
- x-axis = time (in seconds)
- y-axis = distance (in meters)
Therefore:
- The starting position (when t = 0) is the y-intercept.
- The speed of the object (in m/s) is the gradient of the line.
Bus A
Convert Bus A's given speed of 54 km/h into m/s by dividing by 3.6:

Therefore:
- At t = 0, Bus A is at 60 m from the origin.
- It moves with a uniform speed of 15 m/s.
So the y-intercept is (0, 60) and the gradient is 15.
Substitute this information into the slope-intercept form of a linear equation to create an equation representing the motion of Bus A:
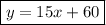
Bus B
Convert Bus B's given speed of 36 km/h into m/s by dividing by 3.6:
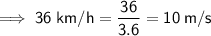
Therefore:
- At t = 0, Bus B is at 160 m from the origin.
- It moves with a uniform speed of 10 m/s.
So the y-intercept is (0, 160) and the gradient is 10.
Substitute this information into the slope-intercept form of a linear equation to create an equation representing the motion of Bus B:

Solution
To find the time when Bus A is at the same position as Bus B, substitute Bus A's equation into Bus B's equation and solve for x:
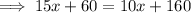
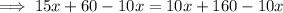
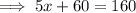
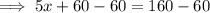
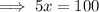
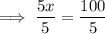
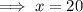
Therefore, the two buses are at the same position 20 seconds after they start moving.
To find their position at this point, substitute x = 20 into one of the equations and solve for y:
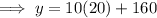
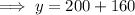
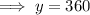
Therefore, the two buses are at the same position at 360 m from the origin.
Conclusion
Bus A overtakes Bus B 20 seconds after they start moving and at 360 m from the origin.