Answer:
Solution: x < -2 or x > 3
Interval notation: (-∞, -2) ∪ (3, ∞)
Explanation:
Given inequality:
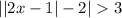
Apply the absolute rule:

Therefore:
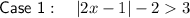
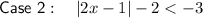
Solve each case independently.
Case 1
Isolate the absolute value on one side of the equation:
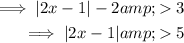
Apply the absolute rule:

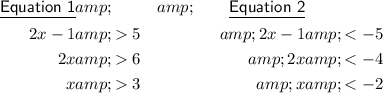
Therefore, x < -2 or x > 3.
Case 2
Isolate the absolute value on one side of the equation:
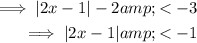
As an absolute value cannot be less than zero, there is no solution for x∈R.
Solution
Solution: x < -2 or x > 3
Interval notation: (-∞, -2) ∪ (3, ∞)