Question

Find the expected value of the winnings

from a game that has the following
payout probability distribution:
Payout ($)
0
2
8
10
Probability 0.35 0.2 0.1 0.2 0.15
Expected Value = [? ]
Round to the nearest hundredth.
Enter

Answer 1

$3.90

Explanation:

Expected Value formula

`\boxed{\displaystytle E(x)=\sum x_iP(x_i)}`

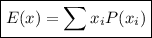
where:

• 
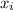  `x_i` is an outcome.
• 
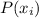  `P(x_i)` is the probability of the outcome.

Given table:

`\begin{array}l \sf Payout\:(\$) & 0 & 2 & 4 & 8 & 10\\\cline{1-6} \sf Probability & 0.35 & 0.2 & 0.1 & 0.2 & 0.15\end{array}`

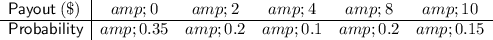
Substitute the given values into the Expected Value formula:

`\begin{aligned}\implies E(x) & = 0(0.35) + 2(0.2)+4(0.1)+8(0.2)+10(0.15)\\& = 0+0.4+0.4+1.6+1.5\\& = 3.9\end{aligned}`

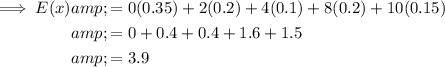
Therefore, the expected value is $3.90.

So, on average, you would expect to receive $3.90 in winnings per game.