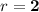Question

Please help with problem 18, Algebra 1, in the attachment

Answer 1

r = 2

Explanation:

To solve this problem, we have to use the following formula for slope:

`\boxed{m= (y_2 - y_1)/(x_2 - x_1)}`,

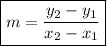where
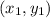`(x_1, y_1)` and
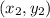`(x_2, y_2)` are the coordinates of two points.

We are given the coordinates
`(r, 3)` and
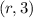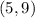`(5, 9)`, and told that
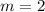`m = 2`. To find the value of r, we have to substitute the given values into the formula and then solve for r :

`2 = (9 - 3)/(5-r)`

⇒
`2 = (6)/(5-r)`

⇒
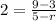
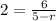
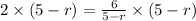`2* (5-r) = (6)/(5-r) * (5 - r)` [Multiplying both sides by (5 - r)

⇒
`2(5-r) = 6`

⇒
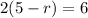
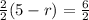`(2)/(2)(5-r) = (6)/(2)` [Dividing both sides by 2]

⇒
`5- r = 3`

⇒
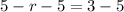`5 - r - 5 = 3 - 5` [Subtracting 5 from both sides]

⇒
`-r = -2`

⇒
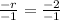`(-r)/(-1)= (-2)/(-1)` [Dividing both sides by -1]

⇒
`r = \bf 2`

Answer 2

r=2

Explanation:

To find the slope, we take the difference in the y values over the difference in the x values

m = ( y2-y1)/(x2-x1)

2 = ( 9-3)/ (5-r)

2 = (6)/(5-r)

Multiply each side by (5-r)

2 ( 5-r) = 6

Divide each side by 2

5-r = 6/2

5-r = 3

Subtract 5 from each side

5-r-5 = 3-5

-r = -2

r = 2