Question

An auditorium has 20 seats in the 1st row, 24 seats on the second row, 28 seats on the third row, and so on up to the 20th row.. How many seats are there in the last row? How many seats are there in the auditorium?​

Answer 1

96 and 1160

Explanation:

1st row → 20

2nd row → 24

3rd row → 28

the number of seats increases by 4 each row.

This indicates an arithmetic progression with common difference d = 4

the nth term of an arithmetic sequence is

`a_(n)` = a₁ + (n - 1)d

where a₁ is the first term and d the common difference

here a₁ = 20 and d = 4 , then

a₂₀ = 20 + (19 × 4) = 20 + 76 = 96

there are 96 seats in the last row

the sum to n terms of an arithmetic sequence where the first and last terms are known is

`S_(n)` =
`(n)/(2)` (first term + last term)

here a₁ = 20 and a₂₀ = 96 , then

S₂₀ =
`(20)/(2)` (20 + 96) = 10 × 116 = 1160

there are 1160 seats in the auditorium

Answer 2

96 seats in the last row.

1160 seats in the auditorium.

Explanation:

The given scenario can be modeled as an arithmetic sequence where the number of seats in each row of the auditorium is the corresponding term in the sequence:

• 20, 24, 28, ...

General form of an arithmetic sequence:

`\boxed{a_n=a+(n-1)d}`

where:

• 
  `a_n` is the nth term.
• a is the first term.
• d is the common difference between terms.

For the given sequence 20, 24, 28, ...

• a = 20
• d = 24 - 20 = 4

Therefore, the equation for the number of seats in the nth row is:

`\boxed{a_n=20+(n-1)4}`

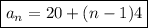
To find the number of seats in the 20th row, substitute n = 20 into the found formula:

`\begin{aligned}\implies a_(20)&=20+(20-1)4\\& = 20+(19)4\\& = 20+76\\& = 96\end{aligned}`

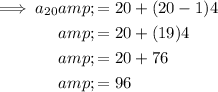
Therefore, there are 96 seats in the last row.

Sum of the first n terms of an arithmetic series:

`\boxed{S_n=(n)/(2)(a+a_n)}`

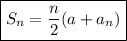
To find the total number of seats in the auditorium, substitute n = 20, a = 20 and a₂₀ = 96 into the formula:

`\begin{aligned}\implies S_(20) & = (20)/(2)(20+96)\\& = 10(116)\\& = 1160\end{aligned}`

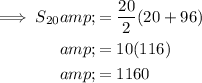
Therefore, there are a total of 1160 seats in the auditorium.