Answer: 1365 combinations
Explanation:
What you're looking for if the order doesn't matter is the number of combinations.
You can use this formula for it:
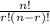
Where n is the number of objects there are and r is the number of objects you take out.
We'll be using the variables:
n = 15
r = 4
Plug them in and solve:
