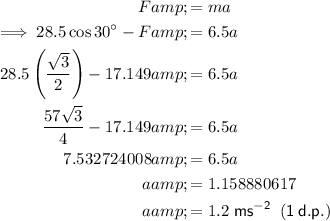Question

100 POINTS!!

A 28.5-Newton force is applied at a 30-degree angle to the horizontal to accelerate a 6.5-kg box across a rough surface (coefficient of friction = 0.22). Use g = 9.8 m/s/s to find frictional force (F(frict)) , normal force (F(norm)) , gravitational force (F(grav)) , and acceleration (a). Enter each answer accurate to the first decimal place.

Answer 1

Frictional force (F(frict)) = 17.1 N

Normal force (F(norm)) = 78.0 N

Gravitational force (F(grav)) = 63.7 N

Acceleration (a) = 1.2 ms⁻²

Explanation:

Newton's second law:

`\boxed{F_(net)=ma}`

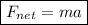
where:

• 
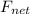  `F_(net)` = overall resultant force.
• m = mass.
• a = acceleration.

Use trigonometry to resolve the 28.5 N force into its horizontal and vertical components since it is acting on the particle at 30°:

`\implies F_x=28.5 \cos 30^(\circ)`

`\implies F_y=28.5 \sin 30^(\circ)`

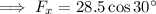
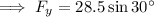
Weight (mg)

Due to the particle's mass, m, and the acceleration due to gravity, g:

`\boxed{W=mg}`

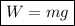
Given:

• m = 6.5 kg
• g = 9.8 ms⁻²

`\begin{aligned}W & = mg\\\implies W & = 6.5 * 9.8\\W & = 63.7\;\sf N\end{aligned}`

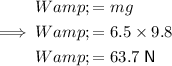
Normal reaction (R)

The particle is moving parallel to the plane (the horizontal), so acceleration perpendicular to the plane is zero.

Resolving forces vertically (taking ↑ as positive):

`\begin{aligned}F & = ma\\\implies R-W-28.5 \sin 30^(\circ)&=6.5 * 0\\R-W-28.5 \sin 30^(\circ)&=0\\R & = W+28.5 \sin 30^(\circ)\\R & = 6.5(9.8)+28.5(0.5)\\R & = 63.7+14.25\\R & = 77.95\\R & = 78.0 \;\; \sf N\; (1\:d.p.)\end{aligned}`

Frictional force (F)

When a moving object is acted on by a frictional force, fiction is limiting, and the frictional force F is at its maximum value:

`\boxed{F = \mu R}`

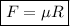
(Where μ is the coefficient of friction and R is the normal reaction).

`\begin{aligned}F & = \mu R\\\implies F & = 0.22 * 77.95\\F & = 17.149\\F & = 17.1 \;\; \sf N\;(2\:d.p.)\end{aligned}`

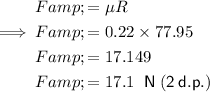
Acceleration (a)

Friction always acts in the opposite direction to motion (or potential motion).

Resolving forces horizontally (taking → as positive):

`\begin{aligned}F & = ma\\\implies 28.5 \cos 30^(\circ)-F & = 6.5a\\28.5 \left((√(3))/(2)\right)-17.149 & = 6.5a\\(57√(3))/(4)-17.149 & = 6.5a\\7.532724008 & = 6.5a\\a & = 1.158880617\\a & = 1.2\; \sf ms^(-2)\;\;(1\:d.p.)\end{aligned}`