Answer:
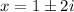
or
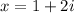
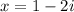
Explanation:
All equations of the form
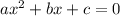 can be solved using the quadratic formula:
can be solved using the quadratic formula:
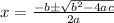
Quadratic formula gives two solutions, one when ± is addition add one when it is subtraction.
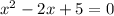
Equation is in standard form:
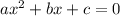
Substitute 1 from a,
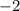 for b, and
for b, and
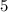 for C in the quadratic formula,
for C in the quadratic formula,
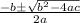
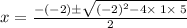
Multiply -4 × 5:
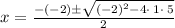
Add 4 + -20:
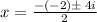
* the opposite of -2 is 2:
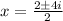
Now, solve equation:
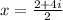
Divide 2 + 4i by 2:
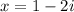
_____________________________