Answer:
The tortoise won the race by approximately
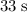 .
.
Step-by-step explanation:
Note that speed in the question is measured in meters-per-second. Apply unit conversion and ensure that times in this question are also measured in seconds:
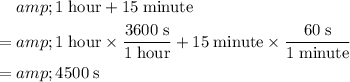 .
.
Time required for the tortoise to finish the race:
 .
.
The time required for the hare to finish the race includes:
- time required to cover
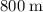 at a speed of
at a speed of
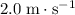 ,
,
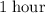 and
and
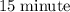 (
(
 ) of nap, and
) of nap, and- time required to cover
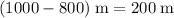 at
at
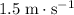 .
.
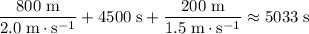 .
.
Therefore, the tortoise wins the race by approximately
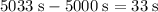 .
.