Find (d^2y)/(dx^2) if x^2y^2=1 Options: A. (2y)/(x^2) B. 0 C. (y)/(x) D. (-y)/(x) E. (-y)/(x^2)

Question

Find
`(d^2y)/(dx^2)` if
`x^2y^2=1`

Options:

A.
`(2y)/(x^2)`
B. 0
C.
`(y)/(x)`
D.
`(-y)/(x)`
E.
`(-y)/(x^2)`

Answer 1

A)
`(d^2y)/(dx^2)=(2y)/(x^2)`

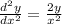
Explanation:

Use implicit differentiation to find dy/dx

`x^2y^2=1\\\\(d)/(dx)(x^2y^2)=(d)/(dx)(1)\\ \\x^2((d)/(dx)y^2)+((d)/(dx)(x^2))y^2 =0\\\\2yx^2(dy)/(dx)+2xy^2=0\\\\2xy(x(dy)/(dx)+y)=0\\ \\x(dy)/(dx)+y=0\\ \\x(dy)/(dx)=-y\\ \\(dy)/(dx)=-(y)/(x)`

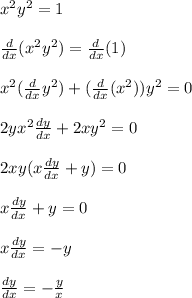
Determine d²y/dx² using dy/dx

`(dy)/(dx)=(-y)/(x)\\ \\ (d^2y)/(dx^2)=((x)[(d)/(dx)(-y)]-(-y)[(d)/(dx)(x)] )/(x^2)\\ \\ (d^2y)/(dx^2)=(-x(dy)/(dx)+y)/(x^2)\\ \\ (d^2y)/(dx^2)=(-x((-y)/(x))+y)/(x^2)\\\\ (d^2y)/(dx^2)=(-(-y)+y)/(x^2)\\\\ (d^2y)/(dx^2)=(y+y)/(x^2)\\\\ (d^2y)/(dx^2)=(2y)/(x^2)`

Helpful tips

• When doing implicit differentiation, make sure to treat "y" as a constant and write dy/dx next to the y-term because it's differentiated with respect to x
• The product rule is
  `(d)/(dx)[f(x)g(x)]=f(x)[(d)/(dx)g(x)]+[(d)/(dx)f(x)]g(x)`
• The quotient rule is
  `(d)/(dx)[(f(x))/(g(x))]=(f(x)[(d)/(dx)g(x)]-g(x)[(d)/(dx)f(x)])/((g(x))^2)`
• 
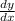  `(dy)/(dx)` represents the first derivative of y with respect to x and
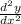  `(d^2y)/(dx^2)` represents the second derivative of y with respect to x

Let me know if you have any more questions!