Question

How to solve that question? ​

Answer 1

(i) (x√x)/3 -(√x)/2

(ii) f(x) = x³/27 +3x -5

Explanation:

You want the value of the integral in each case. One integral is indefinite, the other has conditions specified.

In each case, the power rule applies:

`\displaystyle \int{x^n}\,dx=(x^(n+1))/(n+1)`

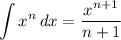
(i) indefinite integral

The integral can be rewritten as the sum of two integrals involving half powers.

`\displaystyle \int{(2x-1)/(4√(x))}\,dx=(1)/(2)\int{x^{(1)/(2)}}\,dx-(1)/(4)\int{x^{-(1)/(2)}}\,dx=\frac{x^{(3)/(2)}}{2\left((3)/(2)\right)}-\frac{x^{(1)/(2)}}{4\left((1)/(2)\right)}\\\\=\boxed{(1)/(3)x√(x)-(1)/(2)√(x)}`

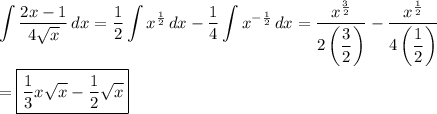
(ii) f'(x)=ax²+b

You are given the derivative and three conditions:

• f'(x) = ax² +b
• f'(3) = 4
• f(3) = 5
• f(0) = -5

Together with the integral, the conditions give rise to three equations in the three unknown coefficients.

`\displaystyle f(x) = \int{ax^2+b}\,dx=(a)/(3)x^3+bx+c`

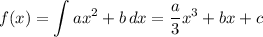
Then the equations we can write for a, b, c are ...

f'(3) = 4 ⇒ a(3²) +b = 4

f(3) = 5 ⇒ (a/3)(3³) +b(3) +c = 5

f(0) = -5 ⇒ a(0³) +b(0) +c = -5

The last equation gives the value of c = -5, so the remaining equations become ...

9a +b = 4

9a +3b = 10

Subtracting the first from the second, we have ...

(9a +3b) -(9a +b) = (10) -(4)

2b = 6

b = 3

Using this in the first equation, we find 'a' to be ...

9a +3 = 4

a = 1/9

Then f(x) is ...

`\boxed{f(x)=(1)/(27)x^3+3x-5}`