Question

Use the initial term and the recursive formula to find an explicit formula for the sequence an. Write your answer in simplest form. an=-2 an = an-1 -13 an=​

Answer 1

From the recursive rule

`a_n = a_(n-1)-13`

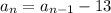
it follows that

`a_(n-1)=a_(n-2)-13 \implies a_n = a_(n-2) - 2*13`

`a_(n-2)=a_(n-3)-13 \implies a_n = a_(n-3) - 3*13`

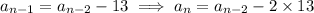
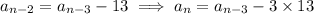
and so on. Notice how the subscript on a on the right side and the coefficient multiplied by 13 add up to n (n - 2 + 2 = n; n - 3 + 3 = n; and so on). If we continue the pattern, we'll end up with

`a_n = a_1 + (n-1)*13`

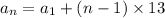
so that the explicit rule for the n-th term in the sequence is

`a_n = -2 + 13(n-1) \implies a_n = \boxed{13n-15}`