Question

The circle below is centred at O.

a) Work out the size of angle x.
b) Which of the circle theorems below allows
you to calculate this angle?
O
X
Not drawn accurately
31°
The perpendicular line from the centre of a circle to a chord
bisects the chord
Two tangents that meet at a point are the same length
The angle at the circumference in a semicircle is a right angle
Opposite angles in a cyclic quadrilateral add up to 180°
The angle between the tangent and the radius at a point
on a circle is 90°

Answer 1

`\textsf{a)} \quad x = 59^(\circ)`

`\textsf{b)} \quad \boxed{\begin{minipage}{8.5 cm}\sf The angle between the tangent and the radius at a point \\on a circle is $90^(\circ)$.\end{minipage}}`

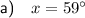
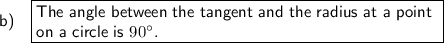
Explanation:

Part (a)

As two sides of the triangle inside the circle are the radius of the circle, the triangle is an isosceles triangle.

Therefore, its two base angles are 31°.

The tangent of a circle is:

• A straight line that touches the circle at only one point.
• Always perpendicular to the radius.

Therefore:

`\implies x + 31^(\circ) = 90^(\circ)`

`\implies x +31^(\circ)-31^(\circ)= 90^(\circ) - 31^(\circ)`

`\implies x = 59^(\circ)`

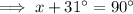
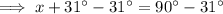
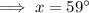
Part (b)

The circle theorem that allows you to calculate angle x is:

`\boxed{\begin{minipage}{8.5 cm}\sf The angle between the tangent and the radius at a point \\on a circle is $90^(\circ)$.\end{minipage}}`