Answers:
- (a) Water decreases at a rate of 16 liters per minute.
- (b) 800 liters
====================================================
Step-by-step explanation:
Part (a)
The rate of change is the same as slope for linear equations such as this one. We know we have a linear equation since it states the water is drained at a constant rate. That constant rate being the slope.
Pick any two columns to form the (x,y) points needed
x = time in minutes
y = number of liters left over
I'll pick the first two columns to get the points (15,560) and (20,480)
Let's find the slope of the line through those points
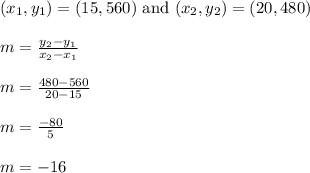
The slope is -16
The slope being negative tells us that as x goes up, y goes down, and vice versa. The variables move in opposite directions.
So as time (x) increases, the amount of water (y) decreases
It decreases by 16 liters per minute. After each minute, the vat has lost 16 liters.
------------------------------
Part (b)
We'll use the slope we found in part (a), which was m = -16
Use any of the columns to form an (x,y) point. I'll use (15, 560)
So x = 15 and y = 560 pair up together
Plug these items into the slope-intercept equation below to solve for the y intercept b

The equation y = mx+b updates to y = -16x+800
The 800 is the initial amount of water. It's when the time is x = 0 minutes.
Therefore, we started off with 800 liters of water.