Question

`\rm \int_( 0)^ {\large\frac{\pi}4} \sqrt{ \tan(x) - \tan {}^(2) (x) } \: dx \\`

Answer 1

First substitute
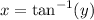`x=\tan^(-1)(y)` to rewrite the integral as

`\displaystyle \int_0^(\pi/4) √(\tan(x) - \tan^2(x)) \, dx = \int_0^1 (√(y-y^2))/(1+y^2) \, dy`

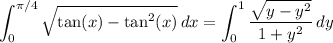
Now use an Euler substitution,
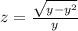`z=\frac{√(y-y^2)}y` to rewrite it again as

`\displaystyle \int_0^(\pi/4) √(\tan(x) - \tan^2(x)) \, dx = 2 \int_0^\infty (t^2)/((t^2+1)^2 + 1) (t^2 + 1)) \, dt`

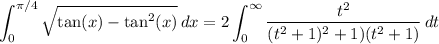
where we take

`√(y - y^2) = √(-y(y-1)) = yt \implies y = \frac1{1+t^2} \text{ and } dy = -(2t)/((1+t^2)^2) \, dt`

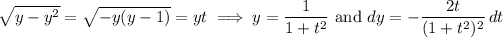
Partial fractions:

`\displaystyle (t^2)/(((t^2+1)^2+1) (t^2 + 1)) = (t^2+2)/(t^4+2t^2+2) - \frac1{t^2+1}`

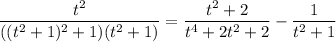
so that

`\displaystyle \int_0^(\pi/4) √(\tan(x) - \tan^2(x)) \, dx = 2 \left(\int_0^\infty (t^2+2)/(t^4+2t^2+2) \, dt - \int_0^\infty (dt)/(t^2+1)\right)`

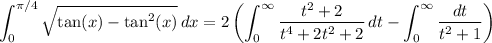
The second integral is trivial,

`\displaystyle \int_0^\infty (dt)/(t^2+1) = \lim_(t\to\infty)\tan^(-1)(t) - \tan^(-1)(0) = \frac\pi2`

For the other, I'm compelled to use the residue theorem, though real methods are doable too (e.g. trig substitution). Consider the contour integral

`\displaystyle \int_\Gamma f(z) \, dz = \int_\Gamma (z^2+2)/(z^4+2z^2+2) \, dz`

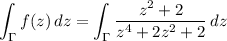
where
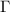`\Gamma` is a semicircle in the upper half of the complex plane, and its diameter lies on the real axis connecting
`-R` to
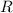`R`. The value of this integral is 2πi times the sum of the residues in the upper half-plane. It's fairly straightforward to convince ourselves that the integral along the circular arc vanishes as
`R\to\infty`, so the contour integral converges to the integral over the entire real line. Note that

`\displaystyle 2 \int_0^\infty (t^2+2)/(t^4+2t^2+2) \, dt = \int_(-\infty)^\infty (t^2+2)/(t^4+2t^2+2) \, dt`

since the integrand is even.

Find the poles of
`f(z)`.

`z^4 + 2z^2 + 2 = 0 \\\\ ~~~~ \implies (z^2+1)^2 = -1 \\\\ ~~~~ \implies z^2 = -1 \pm i \\\\ ~~~~ \implies z = \pm √(-1 \pm i) = \sqrt[4]{2}\, e^(\pm i(3\pi/8 + \pi k))`

where
`k\in\{0,1\}`.

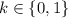The two poles we care about are at
`z_1=\sqrt[4]{2}\,e^(i\,3\pi/8)` and
`z_2=\sqrt[4]{2}\,e^(-i\,11\pi/8)`. Compute the residues at each one.

`\displaystyle \mathrm{Res}\left\{f(z),z=z_1\right\} = \lim_(z\to z_1) (f(z))/(z-z_1) = -\frac1{2^(7/4)}\,ie^(-i\,\pi/8) \\\\ ~~~~~~~~~~~~~~~~~~~~~~~~= -\frac1{2^(7/4)} \left(\sin\left(\frac\pi8\right) + i \cos\left(\frac\pi8\right)\right)`

`\displaystyle \mathrm{Res}\left\{f(z),z=z_2\right\} = \lim_(z\to z_2) (f(z))/(z-z_2) = -\frac1{2^(7/4)}\,ie^(i\,\pi/8) \\\\ ~~~~~~~~~~~~~~~~~~~~~~~~= \frac1{2^(7/4)} \left(\sin\left(\frac\pi8\right) - i \cos\left(\frac\pi8\right)\right)`

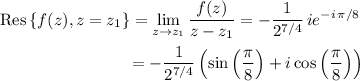
By the residue theorem,

`\displaystyle \int f(z) \, dz = 2\pi i \sum_(\rm poles) \mathrm{Res}\{f(z)\} = (4\pi)/(2^(7/4)) \cos\left(\frac\pi8\right)`

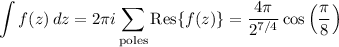
We also have

`\displaystyle \cos^2\left(\frac\pi8\right) = \frac{1 + \cos\left(\frac\pi4\right)}2 = \frac{2 + \sqrt2}4 \implies \cos\left(\frac\pi8\right) = \frac{√(2+\sqrt2)}2`

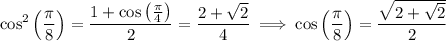
Then the remaining integral is

`\displaystyle \int_0^\infty (t^2+2)/(t^4+2t^2+2) \, dt = (4\pi)/(2^(7/4)) \cos\left(\frac\pi8\right) = \sqrt{\frac12 + \frac1{\sqrt2}} \, \pi`

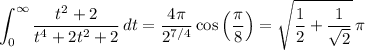
It follows that

`\displaystyle \int_0^(\pi/4) √(\tan(x) - \tan^2(x)) \, dx = \boxed{\left(\sqrt{\frac12 + \frac1{\sqrt2}} - 1\right) \pi}`