Answer:
3. (d) y = 2x + 2
4. (c) 10
5. See attachment.
Explanation:
Slope formula
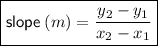
where (x₁, y₁) and (x₂, y₂) are points on the line.
Slope-intercept form of a linear equation
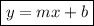
where m is the slope and b is the y-intercept.
Question 3
Given points on the line:
- (x₁, y₁) = (1, 4)
- (x₂, y₂) = (-2, -2)
Substitute the given points into the slope formula to find the slope, m:
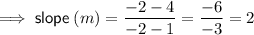
Substitute the found slope and one of the points into the slope-intercept equation and solve for b:
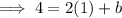

Therefore, the equation of the line is:
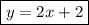
Question 4
Given equation:

Upon comparing the given equation with the slope-intercept formula, the slope of the given line is:
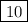
Question 5
The equation y = 2 means that y is 2 for all values of x.
Therefore, to graph y = 2, draw a straight, horizontal line at y = 2.
(See attached graph).