Question

The coordinates of the vertices of quadrilateral are A(-6,-1),B(-5,2),C(-1,-5), and D(0,-2). Parker states that quadrilateral is a parallelogram. Prove or disprove Parker’s statement.

Answer 1

Answer: Parker is correct

=======================================================

Step-by-step explanation:

Use the slope formula to find the slope of the line through A(-6,-1) and B(-5,2)

`(x_1,y_1) = (-6,-1) \text{ and } (x_2,y_2) = (-5,2)\\\\m = (y_(2) - y_(1))/(x_(2) - x_(1))\\\\m = (2 - (-1))/(-5 - (-6))\\\\m = (2 + 1)/(-5 + 6)\\\\m = (3)/(1)\\\\m = 3\\\\`

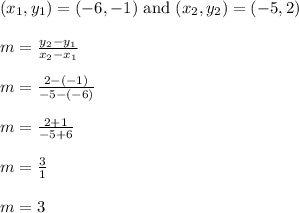
The slope of segment AB is 3.

-------------

Repeat these set of steps for segment CD

C = (-1,-5)

D = (0,-2)

`(x_1,y_1) = (-1,-5) \text{ and } (x_2,y_2) = (0,-2)\\\\m = (y_(2) - y_(1))/(x_(2) - x_(1))\\\\m = (-2 - (-5))/(0 - (-1))\\\\m = (-2 + 5)/(0 + 1)\\\\m = (3)/(1)\\\\m = 3\\\\`

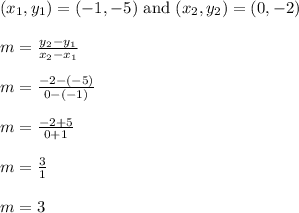
The slope of segment CD is also 3

Parallel lines have equal slopes, but different y intercepts.

Since AB and CD have the same slope of 3, this shows AB is parallel to CD.

--------------

Now find the slope of segment BD

B = (-5,2)

D = (0,-2)

`(x_1,y_1) = (-5,2) \text{ and } (x_2,y_2) = (0,-2)\\\\m = (y_(2) - y_(1))/(x_(2) - x_(1))\\\\m = (-2 - 2)/(0 - (-5))\\\\m = (-2 - 2)/(0 + 5)\\\\m = -(4)/(5)\\\\`

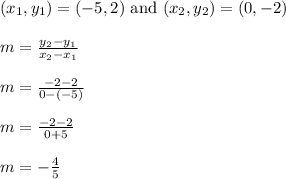
Segment BD has a slope of -4/5

--------------

Lastly, compute the slope of segment AC

A = (-6,-1)

C = (-1,-5)

`(x_1,y_1) = (-6,-1) \text{ and } (x_2,y_2) = (-1,-5)\\\\m = (y_(2) - y_(1))/(x_(2) - x_(1))\\\\m = (-5 - (-1))/(-1 - (-6))\\\\m = (-5 + 1)/(-1 + 6)\\\\m = -(4)/(5)\\\\`

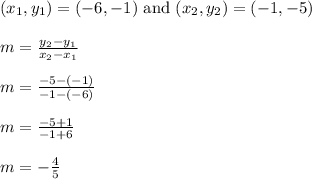
Segment AC has a slope of -4/5

Both segments BD and AC have the same slope of -4/5.

Therefore, segments BD and AC are parallel

----------------

We have two pairs of opposite parallel sides. Ultimately figure ABDC is a parallelogram

See the diagram below.