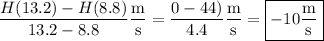The average rate of change of a function
 as
as
 varies from
varies from
 to
to
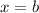 is given by the so-called difference quotient
is given by the so-called difference quotient
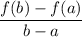
If we plot
 , this difference quotient would correspond to the slope of the line through two points
, this difference quotient would correspond to the slope of the line through two points
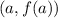 and
and
 and intersecting with the curve
and intersecting with the curve
 .
.
(a) The average rate of change of height from 0 to 6.6 seconds is
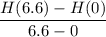
and is measured in m/s.
Consult the table for the values of
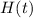 - it tells us
- it tells us
 and
and
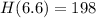 . So the average rate of change of height in this time is
. So the average rate of change of height in this time is
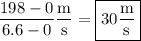
(b) Similarly, the average rate of change of height from 8.8 to 13.2 seconds is