(a) The table clearly shows distance gets smallers as time passes, so the first choice is correct.
Since we know the rate at which the escalator moves is constant, we know that the average rate of change of the escalator's distance from the first floor is the same across any time interval we choose. Take for instance the average rate of change from
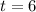 to
to
 . If
. If
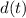 denotes distance at time
denotes distance at time
 , then the average rate of change over these 3 seconds, and at every point in time for that matter, is
, then the average rate of change over these 3 seconds, and at every point in time for that matter, is

In other words, the distance from the first floor is decreasing at a rate of 30 cm/s. (negative sign = decreasing)
(b) At the start, when
 , suppose Alan's distance from the first floor was
, suppose Alan's distance from the first floor was
 . For every second that passes, we know the distance from the first floor decreases by 30 cm. This would mean that after
. For every second that passes, we know the distance from the first floor decreases by 30 cm. This would mean that after
 seconds have passed, the distance would have decreased by a total
seconds have passed, the distance would have decreased by a total
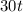 cm.
cm.
This tells us that Alan's distance from the first floor at any time
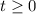 is
is

Using any of the values from the table, we can solve for
 .
.
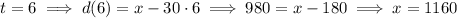
which places Alan 1160 cm = 11.6 m from the first floor at the start.