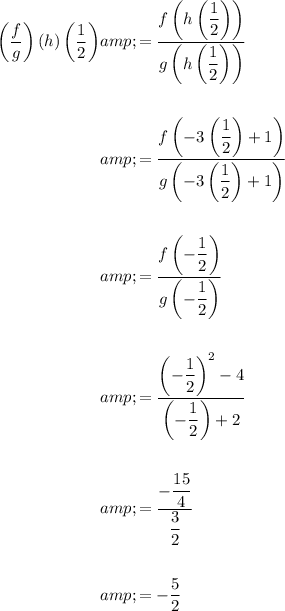Question

Hi can someone help me here​

Answer 1

`\textsf{1.} \quad x^2-2x-1`

`\textsf{2.} \quad -3x^4-5x^3+14x^2+20x-8`

`\textsf{3.} \quad -(5)/(2)`

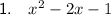
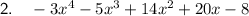
Explanation:

Given functions:

`\begin{cases}f(x) = x^2 - 4\\g(x) = x + 2\\h(x) = -3x + 1\end{cases}`

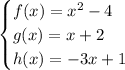
Question 1

The composite function (f + g - h)(x) means to add functions f(x) and g(x) then subtract function h(x):

`\begin{aligned}(f+g-h)(x) & = f(x)+g(x)-h(x)\\& = (x^2-4)+(x+2)-(-3x+1)\\& = x^2-4+x+2+3x-1\\& = x^2+3x+x-4+2-1\\& = x^2+4x-3\end{aligned}`

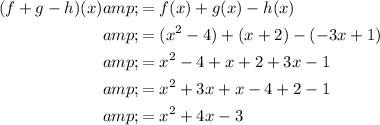
Question 2

The composite function (fgh)(x) means to multiply functions f(x), g(x) and h(x):

`\begin{aligned}(fgh)(x) & = f(x)\cdot g(x) \cdot h(x)\\& = (x^2-4)(x+2)(-3x+1)\\& = (x^2-4)(-3x^2-5x+2)\\& = -3x^4-5x^3+2x^2+12x^2+20x-8\\& = -3x^4-5x^3+14x^2+20x-8\end{aligned}`

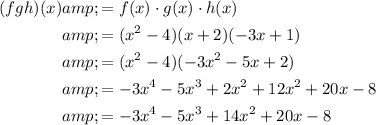
Question 3

The composite function (f/g)(h)(1/2) means to substitute the value of function h(x) when x = 1/2 into function f(x) and function g(x) and divide the former by the latter:

`\begin{aligned}\left((f)/(g)\right)(h)\left((1)/(2)\right) & = (f\left(h\left((1)/(2)\right)\right))/(g\left(h\left((1)/(2)\right)\right))\\\\& = (f\left(-3\left((1)/(2)\right)+1\right))/(g\left(-3\left((1)/(2)\right)+1\right))\\\\& = (f\left(-(1)/(2)\right))/(g\left(-(1)/(2)\right))\\\\& = (\left(-(1)/(2)\right)^2-4)/(\left(-(1)/(2)\right)+2)\\\\& = (-(15)/(4))/((3)/(2))\\\\& = -(5)/(2)\end{aligned}`