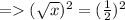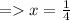Question

Solve square root of x + square root of x+2 = 2

Answer 1

The value of x is
`(1)/(4)`

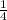
Explanation:

Given:

`√(x) + √(x + 2) = 2`

Rearranging the radical on left side,

`√(x + 2) = 2 - √(x)`

Power on both sides,

`(√(x + 2))^(2) = (2 - √(x))^(2)`

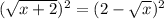
Simplifying the left,

`x + 2 = (2 - √(x) )^(2)`

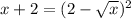
For the RHS equation, use the property of (a-b)² = (a²-2ab+b²),

`= > x + 2 = {2}^(2) - (2 * 2 √(x)) + ( √(x))^(2)`

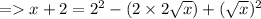
Now calculating its powers,

`= > x + 2 = 4 - 4√(x) + x`

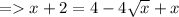
Now sending -4√x to the LHS (left side), its sign becomes plus (+),

`= > 4 √(x) = 4 + x - x - 2`

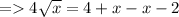
Now the +x and -x will be cancelled,

`= > 4 √(x) = 4 - 2`

`= > 4 √(x) = 2`

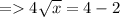
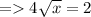
Bringing 4 to the right side, it becomes the denominator,

`= > √(x) = (2)/(4)`

`= > √(x) = (1)/(4)`

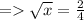
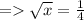
Now powering both sides,

`= > ( √(x))^(2) = ( (1)/(2))^(2)`

`= > x = (1)/(4)`