Answer + Step-by-step explanation:
Part A :
Let M(a , b) be a point where the graphs
of the equations y = 8ˣ and y = 2ˣ⁺² intersect.
M lies on both graphs
Then
the coordinates of M verify both equations (equation of graph1 and equation of graph 2)
Then
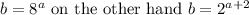
Then
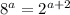
Therefore ‘a’ (the x-coordinates of the points M where the two graphs intersect) is a solution to the equation :
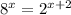
Part B : check the attached table.
Part C :
Graphically, we try to spot the points of intersection of the two graphs ,the x-coordinates of those points are the solution to our equation.
In our case , obviously the two graphs intersect at only one point M(1 ,8)
Therefore 1 is the only solution to 8ˣ = 2ˣ⁺².
Also ,Check the attached graph.