Answer:
$191.29
Explanation:
Use the formula

where P is amount deposited, A the accrued amount, n number of years and r the interest rate in % compounded annually
The division by 100 is necessary to convert r% to a decimal for calculations
We have P = 850, r = 7% and n = 3
Plugging these in we get
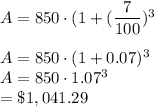
Interest = A - P = 1041.29 - 850 = $191.29