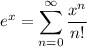Question

Consider the sequence of real numbers


`\rm a_1 = \frac{ log_(2)( {3}^(2) ) }{ log_(3)(2) } ,a_2 = \frac{ log_{ {3}^(3) }( {4}^(4) ) }{ log_{ {4}^3}( {3}^(4) ) } ,a_3 = \frac{ log_{ {4}^5 }( {5}^(6) ) }{ log_{ {5}^(5) }( {4}^(9) ) }, \dots`
In general,
`\rm a_k = \frac{ log_((k + 1) ^((2k - 1)) ) ((k + 2 {)}^(2k)) }{log_((k + 2) ^((2k - 1)) ) ((k + 1 {)}^{ {k}^(2) })}`

Let
`\rm P_n = \frac{ log_{ {(n + 1)}^((2n - 1)) }( {2}^(2n) ) }{ log_{ {2}^((2n - 1)) }((n + 1) {}^{ {n}^(2) } )} \cdot \prod \limits_(k = 1)^(n - 1) a_k` for integer n
`\geq` 2.


`\rm Find \sum \limits_(n = 2)^( \infty ) P_n`
​

Answer 1

Use the change-of-base identity and the exponent property for logarithms.

`\log_b(a) = (\log_c(a))/(\log_c(b)) \implies \log_b(a) = \frac1{\log_a(b)}`

`\log_c(a^b) = b \log_c(a)`

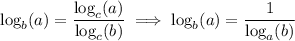
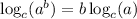
This lets us rewrite

`\log_((k+1)^(2k-1)) (k+2)^(2k) = (2k)/(\log_(k+2)(k+1)^(2k-1)) = (2k)/((2k-1) \log_(k+2)(k+1))`

`\log_((k+2)^(2k-1)) (k+1)^(k^2) = (k^2)/(\log_(k+1) (k+2)^(2k-1)) = (k^2)/((2k-1) \log_(k+1)(k+2))`

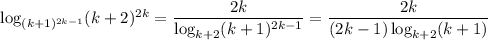
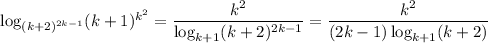
It follows that

`a_k = \frac2k (\log_(k+2)(k+1))/(\log_(k+1)(k+2)) = \frac2k \left(\ln^2(k+1)}{\ln^2(k+2)}`

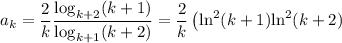
so that the product of
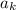`a_k` telescopes:

`\displaystyle \prod_(k=1)^(n-1) a_k = (2^(n-1))/((n-1)!) (\ln^2(2))/(\ln^2(3))\cdot(\ln^2(3))/(\ln^2(4))\cdot(\ln^2(4))/(\ln^2(5)) \cdots (\ln^2(n-1))/(\ln^2(n)) \cdot (\ln^2(n))/(\ln^2(n+1)) \\\\ ~~~~~~~~ = (2^(n-1))/((n-1)!) (\ln^2(n+1))/(\ln^2(2))`

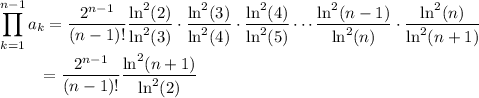
We can similar reduce the coefficient of
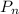`P_n` to write

`\log_((n+1)^(2n-1))(2^(2n)) = (2n)/((2n-1) \log_2(n+1))`

`\log_(2^(2n-1))(n+1)^(n^2) = (n^2)/((2n-1)\log_(n+1)(2))`

`\implies (\log_((n+1)^(2n-1))(2^(2n)))/(\log_(2^(2n-1))(n+1)^(n^2)) = \frac2n (\ln^2(2))/(\ln^2(n+1))`

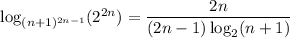
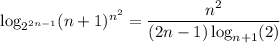
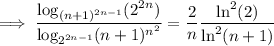
Then the expression for
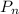`P_n` reduces significantly to

`P_n = \frac2n (\ln^2(2))/(\ln^2(n+1)) \cdot (2^(n-1))/((n-1)!) (\ln^2(n+1))/(\ln^2(2)) = (2^n)/(n!)`

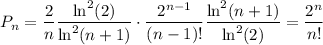
and we ultimately find

`\displaystyle \sum_(n=2)^\infty P_n = \sum_(n=0)^\infty (2^n)/(n!) - (2^1)/(1!) - (2^0)/(0!) = \boxed{e^2 - 3}`

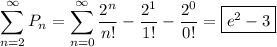
where we recall the power series

`\displaystyle e^x = \sum_(n=0)^\infty (x^n)/(n!)`