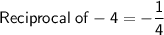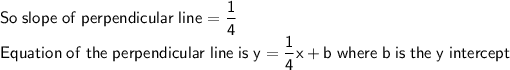Answer:
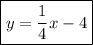
Explanation:
The slope-intercept form of a line equation is y = mx + b

A perpendicular line will have slope is
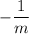
The perpendicular line will have a slope which is the negative of the reciprocal of the first line
Here the line is 4x + y =3
This can be re-written as y = -4x + 3
Slope of this line is -4