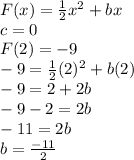Question

the curve with equation y=ax^2+bx+c passes through (0,-1) and has a stationary point of (2,-9). find the values of a, b and c

Answer 1

Explanation:

• 
  `F(x)=ax^(2) +bx+c`
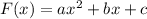
• when we derivate the original general equation
• we get
• 
  `F'(x)=2ax+x`
• For a stationary point we know that the gradient m which in this point is expressed by F'(x) is equal to 0 in the given x coordinate of the stationary point mathematically ⇒F'(2)=0
• When we plug in the x coordinate in our derived equation we have
• 
  `2a(2)+2=0\\4a+2=0\\4a=2\\(4a)/(4) =(2)/(4) \\a=(1)/(2)`
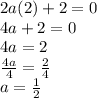
• Therefore we can plug in the value of a we have got in the original equation.
• 
  `F(x)=(1)/(2) x^(2) +bx+c\\`
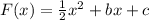
• We have two unknowns in the equation with two points in the function we can use to get the unknowns b and c
• In the F(0)=-1
• 
  `-1=(1)/(2) (0)^(2) +b(0)+c\\c=0`

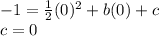
But if we are to check carefully we know that c is the y-intercept wherein x=0 and we already had the point so there was no point of calculating it.

• To get the value of b now substitute/plug in the other point (2,-9) in the equation
• 
  `F(x)=(1)/(2) x^(2) +bx\\c=0 \\F(2)=-9\\-9=(1)/(2)(2)^(2) +b(2)\\ -9=2+2b\\-9-2=2b\\-11=2b\\b=(-11)/(2)`