Question

Identify the volume of the composite figure. Round to the nearest tenth.

Answer 1

860.7 m³ (nearest tenth).

Explanation:

The given composite figure appears to be a rectangular prism with a cylinder omitted.

Volume of a rectangular prism

`V=w\:h\:l`

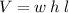
where:

• w = width
• h = height
• l = length

Volume of a cylinder

`V=\pi r^2 h`

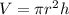
where:

• r = radius
• h = height

Therefore, the formula for the volume of the composite figure is:

`\large\boxed{V=whl- \pi r^2h}`

From inspection of the given diagram:

• w = 10 m
• l = 10 m
• h = 12 m
• r = 3 m

Substitute these values into the formula to find the volume of the composite figure:

`\begin{aligned}\implies V&=whl - \pi r^2h\\& = 10 \cdot 12 \cdot 10- \pi \cdot 3^2 \cdot 12\\& = 120 \cdot 10- \pi \cdot 9 \cdot 12\\& = 1200- 108 \pi\\& = 1200 - 339.292006...\\& = 860.7\; \sf m^3\;(nearest\:tenth)\end{aligned}`

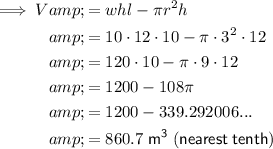
Therefore, the volume of the composite figure is 860.7 m³ (nearest tenth).