Answer: It is not always true, so it's not an identity
========================================================
Step-by-step explanation:
Let's try replacing each 'a' with 1, and each b with 2. Feel free to pick two of your favorite nonzero numbers.
So we'll plug in a = 1 and b = 2
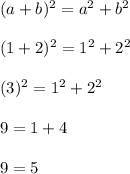
The last equation is a false statement. This means the first equation is also false for a = 1 and b = 2.
This is one counter-example to disprove that (a+b)² = a² + b² is true in general.
Therefore, the equation is not an identity.
--------------
What is an identity however is this
(a+b)² = a² + 2ab + b²
If you were to plug in a = 1 and b = 2, then you'd get 9 on each side. This is one example to help partially confirm it's an identity.
More rigorous proof is in the form of using the FOIL method, the distributive property, or the box method.