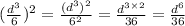1 Answer

Aqueel · Answer 1 · 2023-12-26T23:47:50+0000

Step 1

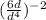
$( \frac{6d}{d {}^(4) } ) {}^( - 2) \\$

Take the reciprocal of the inside to get rid of the negative exponent.

note: reciprocal=flip it over

$( \frac{6d}{d {}^(4) } ) {}^( - 2) = ( \frac{d {}^(4) }{6d} ) {}^(2) \\$

Before we continue we can notice that the inside is reducible since we have d's in the numerator and the denominator.

note: d=d^1

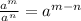
$\frac{a {}^(m) }{a {}^(n) } = a {}^(m - n) \\$

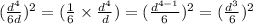
$( \frac{d {}^(4) }{6d} ) {}^(2) =( (1)/(6) * \frac{d {}^(4) }{d}) = ( \frac{d {}^(4 - 1) }{6} ) {}^(2) = ( \frac{d {}^(3) }{6} ) {}^(2) \\$

$note \: that \\ ( ( \omega)/( \eta) ) {}^(x) = \frac{ \omega {}^(x) }{ \eta {}^(x) }$

$( \frac{d {}^(3) }{6} ) {}^(2) = \frac{(d {}^(3)) {}^(2) }{6 {}^(2) } = \frac{d {}^(3 * 2) }{36} = \frac{d {}^(6) }{36} \\$