Question

I will give 100 points

Answer 1

y-intercept = (0, 8)

x-intercepts = (4, 0) and (-2, 0)

vertex = (1, 9)

5th point = (2, 8)

Explanation:

As the coefficient of x² is negative, the curve will be "n" shaped.

y-intercept

crosses the y-axis when x = 0

substitute x = 0 into the function and solve for y:

`\implies y=-(0)^2+(2 * 0)+8=8`

Therefore, y-intercept = (0, 8)

x-intercept

crosses the x-axis when y = 0

set the function to zero and solve for x:

`\implies -x^2+2x+8=0`

`\implies x^2-2x-8=0`

`\implies (x-4)(x+2)=0`

`\implies x=4, x=-2`

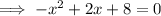
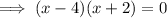
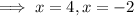
Therefore, x-intercepts = (4, 0) and (-2, 0)

vertex

vertex form:
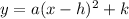`y=a(x-h)^2 +k`, where (h, k) is the vertex

expand vertex equation:
`y=ax^2 -2ahx+ah^2 +k`

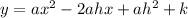
compare coefficients with original function:
`y=-x^2+2x+8`

`\implies a=-1, h=1, k=9`

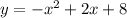
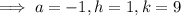
So vertex = (1, 9)

5th plot point

You can choose any value of x and input it into the equation for y, but for symmetry, I have chosen to find the other value of x (aside x = 0) when y = 8

`\implies -x^2+2x+8=8`

`\implies -x^2+2x=0`

`\implies x^2-2x=0`

`\implies x(x-2)=0`

`\implies x=0, x=2`

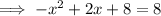
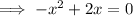
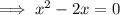
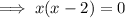
5th point = (2, 8)