There are a couple ways to go about this.
By definition of inverse function, if
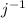 exists, then
exists, then
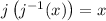
All this means is that if you provide some input
 , plug it into
, plug it into
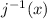 , then plug that into
, then plug that into
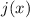 , you end up recovering the original input
, you end up recovering the original input
 that you started with.
that you started with.
We can also do this in the opposite direction, so
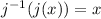
So now if
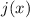 is invertible, then
is invertible, then
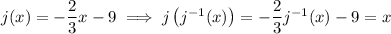
Solve for
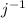 .
.
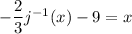
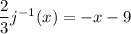
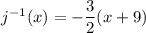
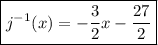
Another way to do it is by algebraically substituting
 within the definition of
within the definition of
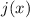
Starting with the given definition

we replace
 with some new expression in a new variable
with some new expression in a new variable
 that makes the right side reduce to just
that makes the right side reduce to just
 . To demonstrate, if we multiply
. To demonstrate, if we multiply
 by
by
 , we end up with a coefficient of 1. So let
, we end up with a coefficient of 1. So let
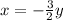 . Then
. Then
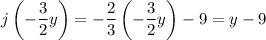
As you can see, this doesn't completely reduce to
 , so we're not done. To adjust for this, we just add 9 to
, so we're not done. To adjust for this, we just add 9 to
 , so our ultimate substitution is
, so our ultimate substitution is
 . Then
. Then
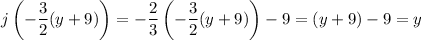
Now applying
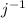 to both sides,
to both sides,
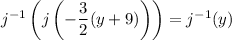
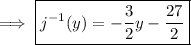
(we can freely swap out
 for
for
 at this point)
at this point)
Yet another way, since the function here is quite simple, we can just think about the action of
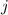 on a given number
on a given number
 - multiply it by -2/3, and subtract 9.
- multiply it by -2/3, and subtract 9.
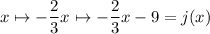
The inverse operation undoes this, so given some number
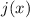 , we recover
, we recover
 by adding the additive inverse of -9, or 9, then multiplying the whole result by the multiplicative inverse of -2/3, or -3/2.
by adding the additive inverse of -9, or 9, then multiplying the whole result by the multiplicative inverse of -2/3, or -3/2.
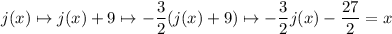
You seem to be using some version of this method. You made the mistake of thinking the "multiply by -3/2" step applies only to
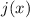 , and not
, and not
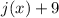 .
.