Question

Factor this 4r³ - 3r²-4r +3

Answer 1

(4r - 3)(r + 1)(r - 1)

Explanation:

In order to factor the polynomial
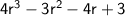`\sf 4r^3 - 3r^2 - 4r + 3`, we can use various factoring methods.
In this case, we can use grouping.

Let's break down the expression and factor it step by step:

Group the terms in pairs:

(4r^3 - 3r^2) +(-4r + 3)

Factor out the greatest common factor from each group:

`\sf r^2(4r - 3) - 1(4r - 3)`

Notice that both groups have a common factor of (4r - 3): and keeping remaining in bracket

`\sf (4r -3)(r^2-1)`

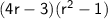
Now, the expression r² - 1 can be factored further using the difference of squares:

(r + 1)(r - 1)

So, the fully factored form of the polynomial 4r³ - 3r² - 4r + 3 is:

(4r - 3)(r + 1)(r - 1)