Question

Pomoże ktoś z matematyki?

Answer 1

Przykład 5.

a) The plot cross the horizontal line
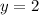`y=2` when the time is
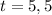`t=5,5`, so it took 5,5 s to cover the first 2 m.

b) If
`f(x)` denotes the distance from the starting position of the object, then its average speed over the entire 6-s period is

`v_(\rm ave) = (3\,\mathrm m - 0\,\mathrm m)/(6\,\mathrm s - 0 \,\mathrm s) = \frac36 (\rm m)/(\rm s) = \boxed{0,5 (\rm m)/(\rm s)}`

c) In the last 3 seconds, the object covers a distance of

`3\,\mathrm m - 1\,\mathrm m = \boxed{2\,\mathrm m}`

d) False. The average speed over the first 3-s period is

`v_(\rm ave[0,3]) = (1\,\mathrm m - 0\,\mathrm m)/(3\,\mathrm s - 0\,\mathrm s) = \frac13 (\rm m)/(\rm s) \approx 0,33 (\rm m)/(\rm s)`

while over the second 3-s period, it is

`v_(\rm ave[3,6]) = (3\,\mathrm m - 1\,\mathrm m)/(6\,\mathrm s - 3\,\mathrm s) = \frac23 (\rm m)/(\rm s) \approx 0,66(\rm m)/(\rm s) \\eq 0,33(\rm m)/(\rm s)`

Przykład 2.

In total there are

8 + 24 + 28 + 16 + 4 = 80

graded assignments. Compute the percentages of students whose scores fall into the given categories:

• 0-8 : 8/80 = 1/10 = 10/100 = 10%

• 9-16 : 24/80 = 3/10 = 30/100 = 30%

• 17-24 : 28/80 = 7/20 = 35/100 = 35%

• 25-32 : 16/80 = 1/5 = 20/100 = 20%

• 33-40 : 4/80 = 1/20 = 5/100 = 5%

See the attached pie chart.

Zadanie 3.

From the plot, it appears that Mateusz

• took 6 min to reach the bus stop

• waited for 2 min

• took 5 min to return home

• took 1 min to grab his notebook

• took 5 min to return to the bus stop

• waited for 3 min

• and after the bus arrives, moves further away over the next 4 min

This means the total time Mateusz needed to (1) return home to get the notebook, (2) find the notebook, and (3) return to the bus stop is

5 min + 1 min + 5 min = 11 min

Zadanie 4.

True. Mateusz walks the distance between his house and the bus stop within the first 6 min, which is 2/5 of 1 km = 0,4 km = 400 m.

True. The bus arrives after 22 min, and its average speed is equal to Mateusz's average speed over the next 4 min. At 22 min, he is 0,4 km from home, and at 26 min, he is 4 km away from home, so the average speed is

`v_(\rm ave) = \frac{4\,\mathrm{km} - 0,4\,\mathrm{km}}{26\,\mathrm{min} - 22\,\mathrm{min}} = \frac9{10} (\rm km)/(\rm min) = 0,9(\rm km)/(\rm min)`

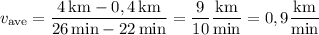
Convert the speed to km/h.

`\frac9{10} (\rm km)/(\rm min) * (60\,\rm min)/(1\,\rm h) = 54 (\rm km)/(\rm h)`