Answer:
c = 5
Explanation:
Slope-intercept form of a linear equation:
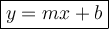
where:
- m is the slope.
- b is the y-intercept.
Given:
- Slope = -¹/₃
- Point = (-1, 0)
Substitute the given slope and point into the formula and solve for b:
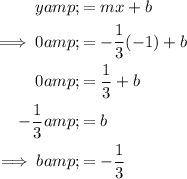
Substitute the given slope and found value of b into the formula to create an equation for the line:
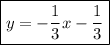
Substitute the point (c, -2) into the equation and solve for c:
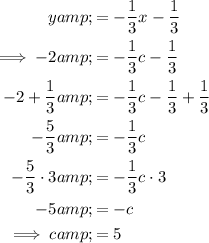
Solution
Therefore, the value of c is 5.