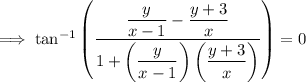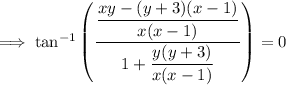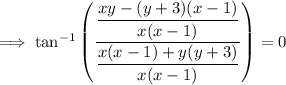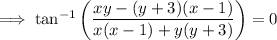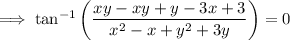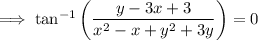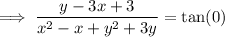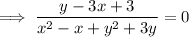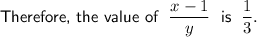Answer:
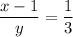
Explanation:
Sums of real and imaginary numbers are known as complex numbers:
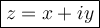
(where x is the real number and iy is the imaginary number).
Complex numbers can be represented on an Argand diagram.
- The x-axis is the real axis.
- The y-axis is the imaginary axis.
z = x + iy is represented on the diagram by the point P(x, y).

It is the angle between the positive real axis and the line joining that number to the origin on an Argand diagram, measured in an anticlockwise direction.

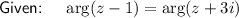

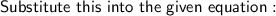
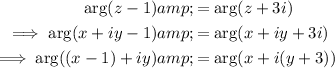
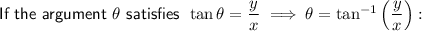
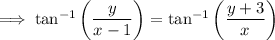
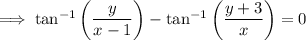
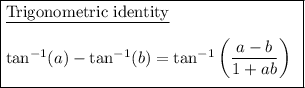
Use the arctan identity: