Question

Find the distance between the points J(-8, 0) and K(1, 4). Answer in simplest exact form.

What’s the exact distance?

Answer 1

distance =
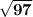`\bf √(97)` units

Explanation:

To find the distance between two points given their coordinates, we can use the following formula:

`\boxed{\mathrm{distance} = √((x_1-x_2)^2 + (y_1 - y_2)^2)}`,

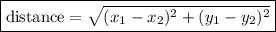where
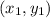`(x_1, y_1)` and
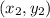`(x_2, y_2)` are coordinates of the two points.

The two points we are given are:

• J(-8, 0)

• K(1, 4).

Using these coordinates and the formula above, we can calculate the distance between the points:

distance =
`√((-8 - 1)^2 + (0 - 4)^2)`

=
`√((-9)^2 + (-4)^2)`

=
`√(81 + 16)`

=
`\bf √(97)`

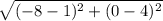
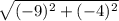
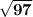
Therefore, the distance between J and K is
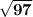`\bf √(97)` units.