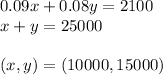let x be the capital invested in the 9% account
let y be the capital invested in the 8% account
let j be the interest earned from the 9% account
let k be the interest earned from the 8% account
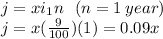
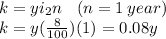
But the total interest made is 2100 $, hence:
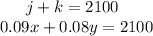
And the total capital invested is 25000 $
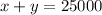
System of 2 equations and two unknowns: