Answer:
8.49673 minutes ≈ 8.5 minutes
Step-by-step explanation:
Acceleration, a is defined as the rate of change in velocity divided by the change in time to attain that velocity
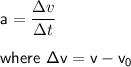 , v = final velocity and v₀ the initial velocity
, v = final velocity and v₀ the initial velocity
and Δt is the time required to attain final velocity
Δt = number of seconds since launch = t since t₀ = 0
Therefore,
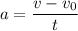
The space shuttle's initial velocity is 0 m/s and its final velocity must be 7800 m/s to escape earth's gravity
So v - v₀ = 7800 - 0 = 7800 m/s, t - t₀ = t = 0 = t seconds
a = 15.3 m/s²
We have the equation
a = 7800/t
a is given as 15.3 m/s² so
15.3 = 7800/t
t = 7800/15.3 = 509.80392 seconds
To convert to minutes, divide by 60
509.80392/60 = 8.49673 minutes ≈ 8.5 minutes