Question

How do we write repeated multiplication as powers and how do we evaluate powers

Answer 1

`5 { \\ }^(2)`

Explanation:

exponents are ways to write multiplication powers 5

`5 {}^(2)`

= 5×5 = 25

Answer 2

• the exponent signifies the number of times the base is a factor
• powers can be evaluated by performing the multiplications

Explanation:

You want to know how multiplication and powers are related, and how powers can be evaluated.

Repeated addition

You may be familiar with the fact that a coefficient is used to signify repeated addition:

y + y + y + y = 4y

The coefficient of 4 in 4y signifies that y is in the sum that many times.

Repeated multiplication

An exponent is used to signify repeated multiplication:

y × y × y × y = y⁴ . . . . y to the fourth power

The exponent of 4 signifies that y is a factor in the product that many times.

In typeset text, the exponent is rendered in a superscript font. In plain text, the exponent (power) is identified using a caret (^):

y⁴ = y^4

Rules of exponents

The rules of exponents derive from the idea of exponents signifying repeated multiplication:

`(x\cdot x)=x^2\\(x\cdot x\cdot x)=x^3\\(x\cdot x)\cdot(x\cdot x\cdot x)=(x\cdot x\cdot x\cdot x\cdot x)\ \Longrightarrow\ x^2\cdot x^3=x^(2+3)=x^5`

Division has a similar rule.

`((x\cdot x\cdot x\cdot x\cdot x))/((x\cdot x))=(x\cdot x\cdot x)\ \Longrightarrow\ (x^5)/(x^2)=x^(5-2)=x^3`

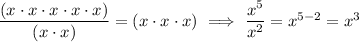
This supports the idea that a positive exponent in the denominator is the same as a negative exponent in the numerator, and vice versa.

Evaluating powers

Powers can be evaluated in a straightforward way by carrying out the multiplications.

In general, the number of significant digits in the result will be the product of the exponent and the number of significant digits in the base.

For example, 9.2^5 could be expected to have 2×5 = 10 significant digits:

9.2^5 = 9.2×9.2×9.2×9.2×9.2 = 65,908.15232

Most calculators are limited to 12 digits or less, and most spreadsheets are limited to 16 digits or less. Some special-purpose calculators have "variable" precision, so are able to properly render higher powers of numbers with more than 1 or 2 significant digits.

A calculator may use any of several techniques for evaluating powers. Among them might be ...

• logarithms
• repeated squaring.

Logarithms

Logarithms turn a power problem into a multiplication problem:

log(9.2^5) = 5·log(9.2)

Of course, once the logarithm is found, the issue of evaluating powers comes back:

9.2^5 = 10^(5×log(9.2)) ≈ 10^(4.818939136727776)

Fortunately, there are methods of evaluating antilogs that simplify this part of raising to a power. The difficulty is that precision may be lost. Here, using the rounded value 10^(4.81893913673) gives the result 65,908.152320337..., which is in error after the 10th digit.

Repeated squaring

An integer power can be written as a sum of powers of 2. For example, ...

37 = 32 +4 +1 = (8 +1)4 +1

Then ...

9.2^37 = (((((9.2^2)^2)^2 · 9.2)^2)^2) · 9.2

This requires only 7 multiplications, not 36

__

Additional comment

Only the first token after the caret is considered to be the exponent:

y^4x = (y^4)(x) . . . . . the first token is 4

y^1/2 = (y^1)/2 = y/2 . . . . the first token is 1

If the exponent has multiple parts, they should be enclosed in parentheses:

`y^(3x+1)`

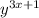
will be written in plain text as ...

y^(3x+1)

and ...

y^(1/2) = √y

You also need to be careful writing multiple exponents using the caret symbol. Parentheses are usually required. The Order of Operations has you evaluate multiple exponents right to left.

3^4^5 = 3^(4^5) = 3^1024

(3^4)^5 = 3^20