Answer:
D)

Explanation:
A function is odd if its graph is symmetric to the origin, which we can check this if
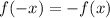 is true:
is true:
Option A
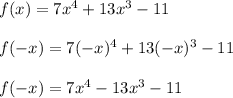
Since
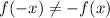 , then the function does not have odd symmetry
, then the function does not have odd symmetry
Option B
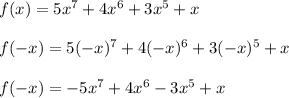
Since
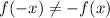 , then the function does not have odd symmetry
, then the function does not have odd symmetry
Option C
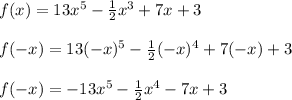
Since
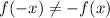 , then the function does not have odd symmetry
, then the function does not have odd symmetry
Option D
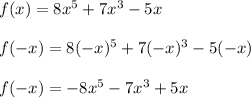
Since
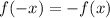 , then the function DOES have odd symmetry. You can also see that the function is odd because every term has an odd exponent.
, then the function DOES have odd symmetry. You can also see that the function is odd because every term has an odd exponent.