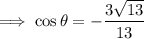Answer:
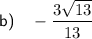
Explanation:
Trigonometric ratios
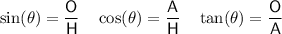
where:
- θ is the angle.
- O is the side opposite the angle.
- A is the side adjacent the angle.
- H is the hypotenuse (the side opposite the right angle).
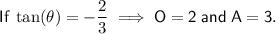
Use Pythagoras Theorem to calculate the length of the hypotenuse:
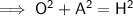
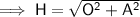
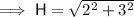
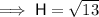
Therefore, substituting the values of A and H into the cosine ratio:
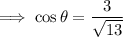
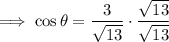
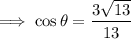
As the terminal side of the angle is in Quadrant II, and cosine is negative in Quadrants II and III, the exact value of cos(θ) is: