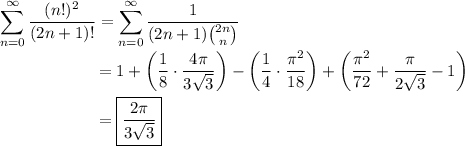Question

`\displaystyle \rm \sum_(n = 0)^ \infty \frac{(n! {)}^(2) }{(2n + 1)!}`​

Answer 1

Observe that

`((n!)^2)/((2n+1)!) = (n!(2n-n)!)/((2n+1)(2n)!) = \frac1{(2n+1)\binom{2n}n}`

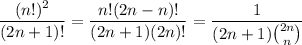
Starting with a well-known series

`\displaystyle 2\arcsin^2(x) = \sum_(n=1)^\infty \frac{(2x)^(2n)}{n^2 \binom{2n}n}`

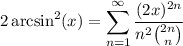
we take some (anti)derivatives to find a sum that more closely resembles ours.

Let
`f(x)=2\arcsin^2(x)`. Then

`\displaystyle f'(x) = 2 \sum_(n=1)^\infty \frac{2^(2n) x^(2n-1)}{n \binom{2n}n}`

`\displaystyle x f'(x) = 2 \sum_(n=1)^\infty \frac{2^(2n) x^(2n)}{n \binom{2n}n}`

`\displaystyle x f''(x) + f'(x) = 4 \sum_(n=1)^\infty \frac{2^(2n) x^(2n-1)}{\binom{2n}n}`

`\displaystyle x^2 f''(x) + x f'(x) = 4 \sum_(n=1)^\infty \frac{2^(2n) x^(2n)}{\binom{2n}n}`

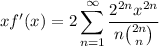
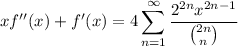
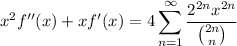
Noting that both sides go to zero as
`x\to0`, by the fundamental theorem of calculus we have

`\displaystyle \sum_(n=1)^\infty \frac{2^(2n) x^(2n+1)}{(2n+1)\binom{2n}n} = \frac14 \int_0^x (t^2 f''(t) + t{}f'(t)) \, dt`

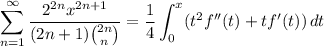
so that when
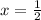`x=\frac12`, and rearranging some factors and introducing a constant, we recover a useful sum.

`\displaystyle \sum_(n=0)^\infty \frac1{(2n+1)\binom{2n}n} = 1 + \frac12 \int_0^(1/2) (x^2 f''(x) + x f'(x)) \, dt`

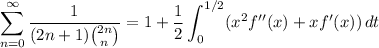
Integrate by parts.

`\displaystyle \int_0^(1/2) x^2 f''(x) \, dx = \frac14 f'\left(\frac12\right) - 2 \int_0^(1/2) x f'(x) \, dx`

`\displaystyle \int_0^(1/2) x f'(x) \, dx = \frac12 f\left(\frac12\right) - \int_0^(1/2) f(x) \, dx`

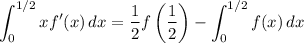
Then our sum is equivalent to

`\displaystyle \sum_(n=0)^\infty \frac1{(2n+1)\binom{2n}n} = 1 + \frac18 f'\left(\frac12\right) - \frac14 f\left(\frac12\right) + \int_0^(1/2) \arcsin^2(x) \, dx`

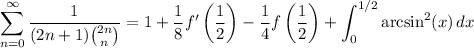
The remaining integral is fairly simple. Substitute and integrate by parts.

`\displaystyle \int_0^(1/2) \arcsin^2(x) \, dx = \int_0^(\pi/6) u^2 \cos(u) \, du \\\\ ~~~~~~~~~~~~~~~~~~~~~~~~~ = (\pi^2)/(72) - 2 \int_0^(\pi/6) u \sin(u) \, du \\\\ ~~~~~~~~~~~~~~~~~~~~~~~~~ = (\pi^2)/(72) + \frac\pi{2\sqrt3} - 2 \int_0^(\pi/6) \cos(u) \, du \\\\ ~~~~~~~~~~~~~~~~~~~~~~~~~ = (\pi^2)/(72) + \frac\pi{2\sqrt3} - 1`

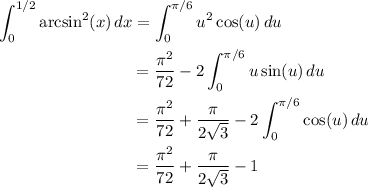
Together with

`f\left(\frac12\right) = 2 \arcsin^2\left(\frac12\right) = (\pi^2)/(18)`

`f'\left(\frac12\right) = \frac{4\arcsin\left(\frac12\right)}{\sqrt{1-\frac1{2^2}}} = (4\pi)/(3\sqrt3)`

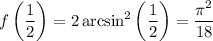
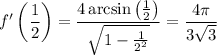
we conclude that

`\displaystyle \sum_(n=0)^\infty ((n!)^2)/((2n+1)!) = \sum_(n=0)^\infty \frac1{(2n+1)\binom{2n}n} \\\\ ~~~~~~~~~~~~~~~~~~ = 1 + \left(\frac18\cdot(4\pi)/(3\sqrt3)\right) - \left(\frac14\cdot(\pi^2)/(18)\right) + \left((\pi^2)/(72) + \frac\pi{2\sqrt3} - 1\right) \\\\ ~~~~~~~~~~~~~~~~~~ = \boxed{(2\pi)/(3\sqrt3)}`