Answer:
59.3° (nearest tenth)
Explanation:
Cosine Rule (for finding angles)
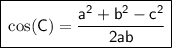
where:
- C = angle
- a and b = sides adjacent the angle
- c = side opposite the angle
From inspection of the given triangle:
- C = angle G
- a = side GI = 6
- b = side GH = 15
- c = side HI = 13
Substitute the values into the formula and solve for G:
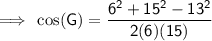
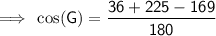
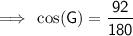
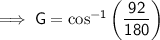
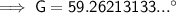
Therefore, the measure of angle G is 59.3° (nearest tenth).