Answer:
See below
Explanation:
A function is continuous within an interval if its first derivative exists
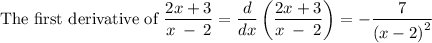
Let's call this first derivative g(x)
g(x) is defined at all values of x except at x=2 since at this value the denominator becomes 0 and g(x) is not defined.
So the function has a discontinuity at x = 2
But in the interval (2, ∞ ) the function g(x) always has a real value so f(x) is continuous in that interval